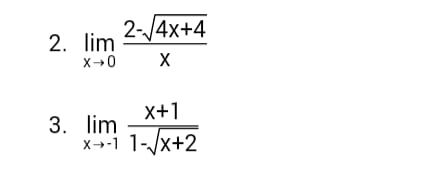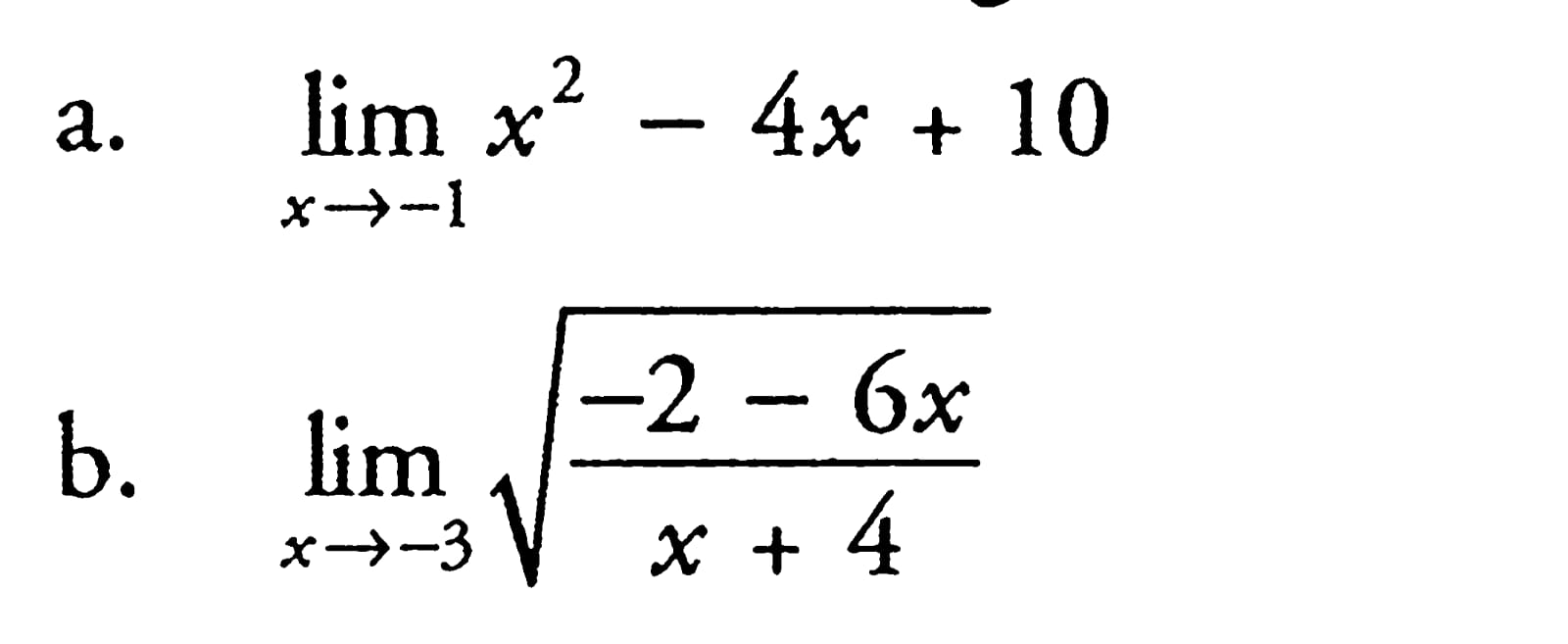
Limit aljabar adalah konsep dalam kalkulus yang digunakan untuk menentukan nilai suatu fungsi ketika variabel mendekati titik tertentu, baik dalam bentuk bilangan hingga maupun tak hingga. Limit ini dapat dihitung menggunakan berbagai metode, seperti substitusi langsung, pemfaktoran, kali sekawan, atau aturan L'Hôpital jika berbentuk tak tentu (jika disubstitusi bernilai 0/0), namun untuk memahami aturan L'Hôpital diperlukan pehamaman terhadap konsep derivatif terlebih dahulu. Sebelum melanjutkan ke metode-metode penyelesaian limit fungsi aljabar lebih lanjut, cermatilah sifat-sifat limit fungsi aljabar ini.

Untuk memahami berbagai metode penyelesaian limit fungsi aljabar, perhatikan penjelasan dibawah ini.
1. Metode Substitusi
Metode substitusi dapat digunakan pada masalah limit aljabar yang jika nilai limit x disubstitusi tidak menghasilkan nilai 0/0, untuk memahami lebih lanjut perhatikan contoh dibawah ini :
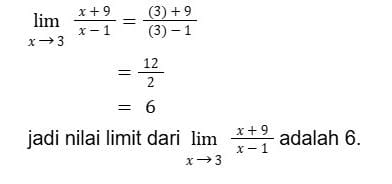
Coba kerjakan contoh soal berikut
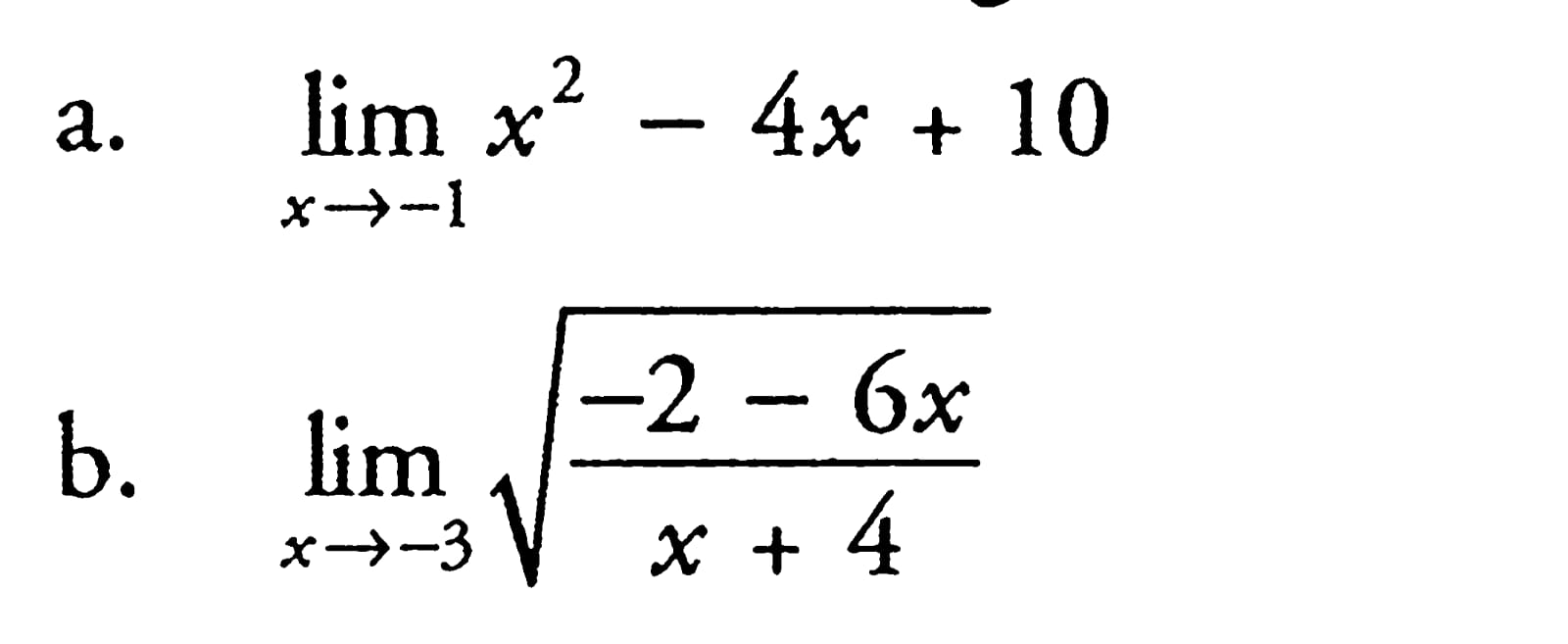
2. Metode Pemfaktoran
Metode ini digunakan pada saat metode substitusi menghasilkan nilai 0/0 atau tidak terdefinisi. sebagai contoh perhatikan penjelasan dibawah ini :
Diberikan sebuah limit
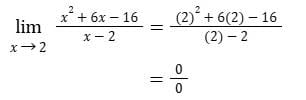
Jika menggunakan metode substitusi akan mendapat hasil yang tidak terdefinisi yaitu 0/0 , maka dari itu diperlukan metode pemfaktoran untuk menentukan nilai limit dari fungsi diatas seperti berikut.
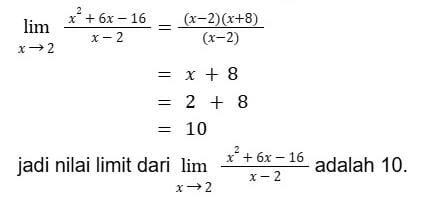
Coba kerjakan contoh soal berikut
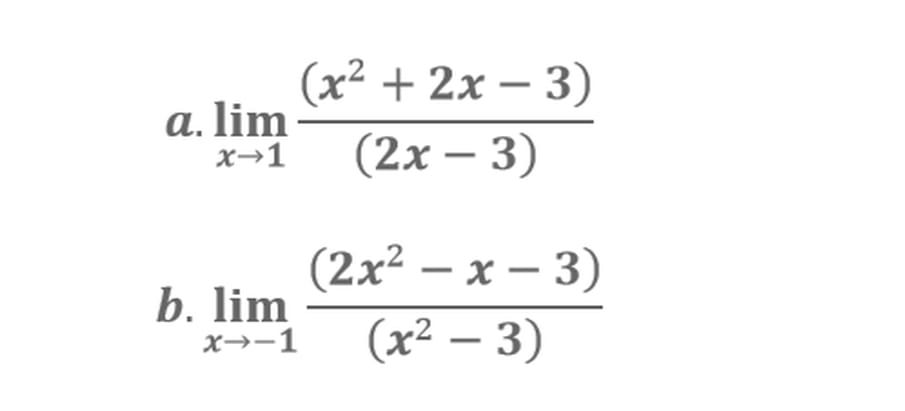
3. Metode Kali Sekawan (Rasionalisasi Penyebut)
Metode kali sekawan digunakan pada saat penyebut dari sebuah limit fungsi aljabar berbentuk akar sehingga perlu untuk dirasionalkan, supaya tidak menghasilkan nilai 0/0. Sebagai contoh perhatikan penjelasan dibawah ini :
Diberikan sebuah limit

Coba kerjakan contoh soal berikut